Let me set the scene:
It's a boring Sunday afternoon and your friend is at your apartment flipping between football games. He sees a deck of cards on your TV stand and proposes a game: You pick black cards or red cards. He deals 7 cards. If there are four or more red cards, red wins, and if there are four or more black cards, black wins. Are you in? Why bother, you think. Why not just flip a coin? But then you remember: the ace of spades isn't in the pack. It's in your bookshelf, sandwiched between pages of a book your dad gave you for your birthday. You take red cards.
This is edge. Your friends think that the odds are 50/50, but they're not. There is a 49.01% chance of drawing a black card and a 50.98% chance of drawing a red card, but this 7 card series swings the odds even harder in your favor. To calculate the probability of red cards winning the game we need to whip out some advanced math: binomial coefficients and the hypergeometric distribution. Binomial coefficients determine how many different ways there are to draw a a number of items from a set: nCr is read as "n choose r" because we are solving how many different ways there are to choose a subset of r elements from a set of n elements. The hypergeometric distribution describes this situation: d draws without replacement from a population size C where each draw is either a success or a failure. I'll bring the rest of this math to the blackboard.
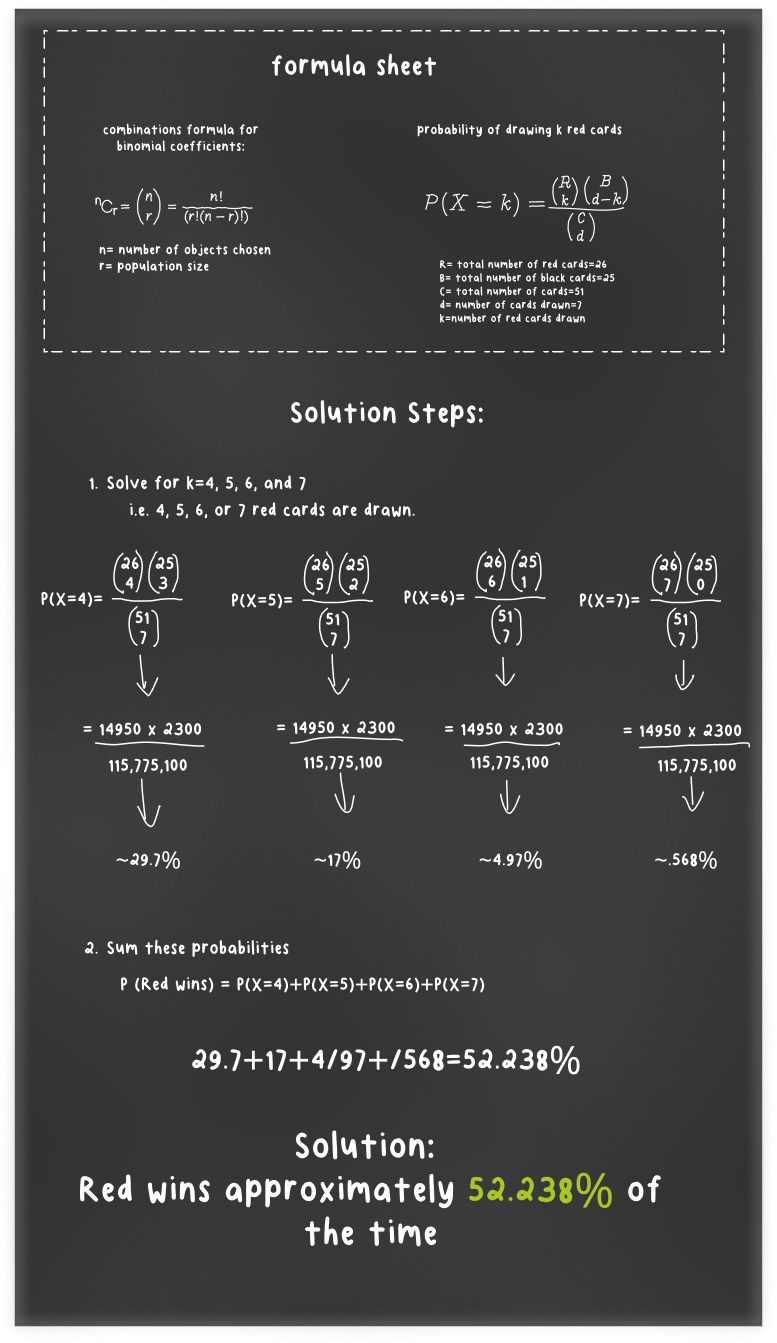
Your friend is giving you 50% odds for an outcome that is actually 52.238% likely to happen. You're getting even odds when you should be getting roughly-109 odds. Anytime you (the bettor) has an advantage over the book, you have edge.
How does this apply to sports betting?
With sports betting there is no "true probability" like there is with a deck of cards or a random number generator, but if you're a computer you can crunch the numbers and figure out what the market considers the truest fairest odd or probability. The majority of the time books are giving you a worse odd than the truest and fairest odds. But sometimes books do offer odds that are better (more favorable) than the truest and fairest off. When this happens, run - don't walk - to take advantage of this bet.
Expected Value (EV+)
You gotta remember that when a gambler says they have edge this is not the same thing as a gambler saying they are guaranteed a win. Having edge simply means that you are more likely than not to win. Imagine you and a rival are rolling a die and you win on 1-5 and your rival wins on 6, at even odds. Your rival can win on any random toss - unlikely things do happen.
But now imagine you and your rival are locked in a sci-fi room for infinity years, throwing the die over and over again. In that sci-fi room you will win, and we can calculate how much you will win. For every $100 you stake on this totally unfair dice game, you can be expected to win $66.67. So if you play the game 1,000 times, staking $100 at even odds every time, you can plan to walk out of that room with a profit of roughly $66,670. You should play as many times as your rival is willing to and you should stake everything you have.
Also remember that being likely to win doesn't mean that the outcome you bet on is likely to happen. It means that the odds you took for that outcome are better than the true odds. This time imagine that you win when the die rolls a six and your rival wins on 1-5. Imagine that your rival gave you +600 odds, representing that your will win only ever 1 in 7 rolls, you still have edge even though your outcome happens far less than 50% of the time. The expected value of this scenario is $16.67 for every $100 you bet.
How To Calculate EV and Edge
The equation for expected value is very intuitive:
((Probability of Winning) x ($Profit per Bet)) - ((Probability of Losing) x ($Loss per Bet))
Let's imagine we are staking $100 on our 51-card-deck card game. Our expected value is $4.48.
Edge is the percent of your stake that you can expect to win as profit on your wager, or Expected Value / Stake. If you don't epect to win money on your wager then you don't have edge.
In our 51 card deck card game your edge is 4.48%
Tools
When you know the truest fair win probability you can use our Expected Value & Edge Calculator.
And sign up for Odder so you can sort bets by edge.

